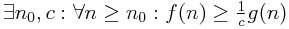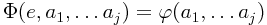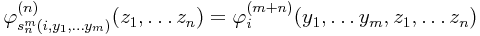Poznámky k IB107

Věta o numeraci

Pro každé j ≥ 1 existuje vyčíslitelná funkce Φ : N^j + 1 → N, která je univerzální pro standardní numeraci j-árních funkcí. Tedy pro každé e ∈ N a (a₁, …a_j) ∈ N^j platí

Pro každou aritu tedy existuje funkce Φ, která bere o jeden argument víc – potřebuje ještě index programu, který má simulovat. Důkaz věty spočívá v definici interpretu – programu, který bude simulovat jiné programy.

Věta o parametrizaci

Ke každému n ≥ 1, m ≥ 1 existuje totálně vyčíslitelná funkce s^m_n : N^m + 1 → N, taková, že platí

Takže: existuje funkce s, která pro index programu i a m jeho argumentů spočítá index jiného programu, který bude dělat totéž co i, ale bude potřebovat o m argumentů méně. Funkce s vlastně zafixuje prvních m argumentů na nějaké konstanty. m je tady počet fixovaných parametrů, n počet těch, které se nefixují.

Dokazuje se pomocí programu, který celou konstrukci realizuje – má m konstant a přesypává argumenty tak, aby to sedělo. Prvních n argumentů posune o m pozic doprava a na uvolněná místa dosadí konstanty. Pozor, aby se při posunování nepřepsalo něco, co bude ještě potřeba.

První Riceova věta

Nechť I ⊂ N je netriviální (není prázdná ani se nerovná N) a rekurzivní. Potom existují indexy programů i ∈ I a j ∈ I′¹ tak, že ϕ_i = ϕ_j.

Tedy pokud je netriviální podmnožina N rekurzivní, potom nerespektuje funkce a naopak pokud nějaká množina respektuje funkce a je netriviální, potom nemůže být rekurzivní.

Důkaz se provede sporem: předpokládejme, že množina respektuje funkce a že množina I obsahuje index nějaké vyčíslitelné funkce² θ, která není prázdná. I′ potom obsahuje indexy prázdné funkce. Kdyby tomu tak nebylo, tak se prohodí I a I′.

Nechť P_f(i) je program begin x₂ := Φ(i, i); x₁ := θ(x₁) end. Zřejmě program P počítá funkci θ, pokud ϕ_i(i) je definované a jinak počítá prázdnou funkci.

Tedy pro všechna i ∈ N platí ϕ_f(i) = θ právě tehdy když i ∈ K.

Pokud tedy f(i) ∈ I, pak f(i) není index prázdné funkce. Je to index θ. Obráceně pokud f(i) je indexem funkce θ, pak f(i) ∈ I. Nechť χ_I je charakteristická funkce I. Pro všechna i ∈ N musí platit

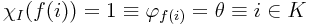
Protože χ_I ∘ f je totálně vyčíslitelná, musela by K být rekurzivní, což zřejmě není.

Druhá Riceova věta

Necht I ⊂ N respektuje funkce a nechť existuje funkce θ taková, že všechny její indexy jsou v I a má vyčíslitelné rozšíření θ′ takové, že jeho indexy patří do I′.

I potom není rekurzivně spočetná.

Důkaz půjde zase sporem. Nechť funkce ξ(i, j) se rovná θ′(j), pokud ϕ_i(i) je definováno a jinak se rovná θ(j). Tato funkce je vyčíslitelná³. Podle věty o parametrizaci existuje totálně vyčíslitelná funkce f : N → N taková, že ξ(i, j) = ϕ_f(i)(j). f(i) potom patří do I právě tehdy, když ϕ_i(i) není definováno. Tj. f(i) ∈ I ≡ i ∈ K′.

Pokud by tedy I byla rekurzivně spočetná, tak i K′ by musela být rekurzivně spočetná. To ale není.

Při použití druhé Riceovy věty je tedy zřejmě potřeba zvolit θ tak, aby nebyla totální. Jinak by totiž neměla potřebné rozšíření.

Třetí Riceova věta

Nechť I ⊂ N respektuje funkce a nechť existuje funkce θ taková, že všechny její indexy patří do I a navíc všechna její konečná zúžení patří do I′.

I potom není rekurzivně spočetná.

Důkaz se opět provede sporem. Nechť funkce μ(i, j) počítá θ(j), pokud P_i nezastaví pro vstup i během nejvýše j kroků. Pokud zastaví během nejvýše j kroků, μ se zacyklí. Funkce μ je zřejmě vyčíslitelná.

Podle věty o parametrizaci existuje totálně vyčíslitelná funkce f tak, že μ(i, j) = ϕ_f(i)(j).

Dostaneme tedy, že pokud i ∈ K, tak P_i zastaví pro i. Tedy existuje j takové, že P_i zastaví pro i po přesně j krocích. Tj. existuje j takové, že ϕ_f(i)(x) počítá θ(x) pro všechna x menší než j a jinak je nedefinované. Potom ale ϕ_f(i) je zúžením θ a její definiční obor je konečný, tedy ϕ_f(i) ∈ I′.

Z druhé strany platí, že když i ∈ K′, tak P_i nikdy nezastaví a ϕ_f(i) počítá celou θ a tedy patří do I.

Tedy i ∈ K′ ≡ f(i) ∈ I a I nemůže být rekurzivně spočetná.

Třetí Riceovu větu tedy zřejmě nejde použít, pokud I obsahuje prázdnou funkci. Ta je totiž konečným zúžením každé funkce.

Časová složitost

f ∈ O(g)

Funkce f roste nejvýše tak rychle jako g.

∃c, n₀ : ∀n ≥ n₀ : f(n) ≤ cg(n)

f ∈ o(g)

Funkce f roste pomaleji než g

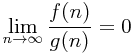
f ∈ Ω(g)

Funkce f roste alespoň tak rychle jako g