CPO a spojité funkce

Každý typ se dá charakterizovat jako částečně uspořádaná množina hodnot. Pokud platí, že každý spočetný řetězec má supremum, potom se jedná o Complete Partial Order.

Primitivní typy – příklady

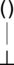
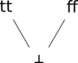
Značky tt a ff jsou jednoduše symboly pro pravdivou a nepravdivou hodnotu. Další primitivní typ je třeba typ všech celých čísel Int.

Operace nad typy

Z primitivních typů je možné pomocí operací vytvářet další, bohatší typy.

Lift X

přidá ⊥ jako nejméně definovaný prvek do typu X. Dno (⊥) je menší než všechny původní prvky v X a jinak se touto operací uspořádání nemění.

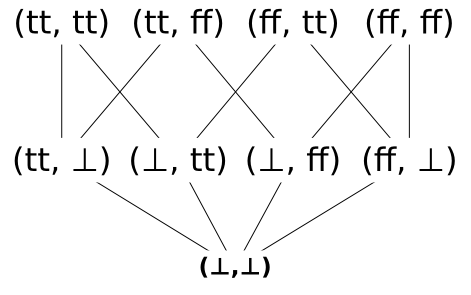
X × Y

kartézský součin dvou typů (typ všech dvojic, kde první složka je typu X a druhá složka má typ Y). Pokud x₁, x₂ ∈ X, x₁ ≤ x₂ a y₁, y₂ ∈ Y, y₁ ≤ y₂, potom platí (x₁, y₁) ≤ (x₂, y₂). ¹

X + Y

disjunktní sjednocení, hodnota tohoto typu obsahuje buď nějakou hodnotu typu X, nebo hodnotu typu Y (např. takto funguje union v C nebo Either v Haskellu)

X → Y

mocninný typ; typ všech spojitých funkcí, které hodnotu typu X zobrazí na hodnotu typu Y

Další příklady jsou ve slidech z přednášky na straně 167.

Spojitost funkce

Funkce f je monotonní právě tehdy, když platí ∀a, b : a ≤ b ⇒ f(a) ≤ f(b).

Tedy: funkce f je monotonní, pokud pro každé dva prvky jejího definičního oboru platí, že pokud je jeden méně definovaný než jiný, tak potom jejich obrazy na tom budou stejně.

Takže například funkce f je monotonní, ale funkce g monotonní není.

f () = True
f ⊥ = True

g () = True
g ⊥ = False

Spojitost funkce je ještě trochu silnější pojem. Každá spojitá funkce je i monotonní. Obrácené tvrzení neplatí, existují i nespojité monotonní funkce. Platí ale, že každá monotonní funkce s konečným definičním oborem (doménou) je spojitá².

Funkce f je spojitá, pokud pro každý spočetný řetězec x₁, x₂, … platí f(⨆(x₁, x₂, …)) = ⨆(f(x₁), f(x₂), …)

(Značka ⨆ značí supremum, nejmenší horní závoru, least upper bound. Horní závora nějaké podmnožiny je prvek, který je větší než libovolný prvek dané podmnožiny.)

Definice tedy říká, že obraz suprema libovolného řetězce musí být supremem obrazů jednotlivých prvků řetězce.

Česky: pokud se vezme libovolný spočetný řetězec a funkcí f zobrazíme jeho supremum, tak musíme dostat totéž, jako kdybychom postupně zobrazili všechny prvky daného řetězce a našli supremum obrazů.

Všechny Unit_⊥ → Bool_⊥

Zadání: Napište všechny spojité funkce typu Unit_⊥ → Bool_⊥. Co je to funkce s tímto typem? Takováto funkce musí každé hodnotě z Unit_⊥ přiřadit něco z Bool_⊥.

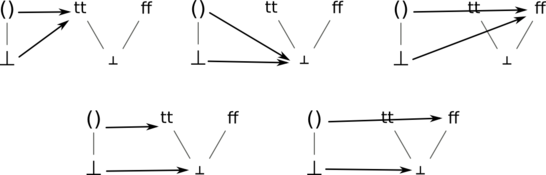
Tyto funkce by bylo vhodné taky seřadit do diagramu, aby bylo patrné, jak to uspořádání na nich funguje. Pro jednoduchost je každou funkci možné zakreslit jako diagram ve tvaru definičního oboru, kde se místo původních prvků na stejná místa doplní hodnota, na kterou se ten který prvek zobrazí.

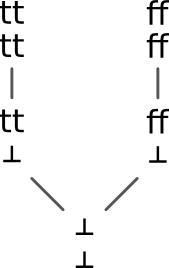
Pro jiný typ funkcí to může dopadnout třeba tak, jako na obrázku níž.

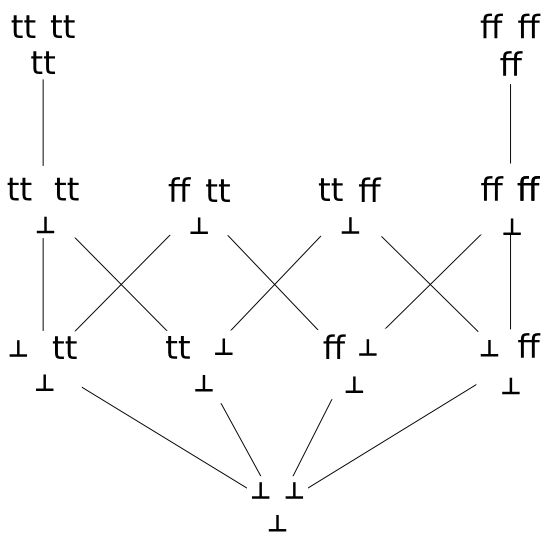
Striktní funkce

Striktní funkce je taková funkce, která nejdříve vyhodnotí svůj argument a potom s ním teprve něco počítá. Pokud je tedy argument nedefinovaný, nemůže být definovaný ani výsledek výpočtu. Pro striktní funkci tedy platí f ⊥ = ⊥.

Odkazy

1. Hussling Haskell types into Hasse diagrams
2. Gin and monotonic
3. Getting a fix on fixpoints