Derivací k regulárním výrazům

V předmětu PV030 se člověk mimo jiné potká s algoritmy pro práci s regulárními výrazy. Jedním z nich je i metoda konverze regulárního výrazu na konečný automat, a ne nedeterministický s ϵ-kroky. Touto metodou je možné rovnou vyrobit minimální deterministický konečný automat. A jak lépe porozumět algoritmu než si ho zkusit naprogramovat?

Podrobnější popis je algoritmu je k dispozici ve slidech, případně ve článku Derivatives of Regular Expressions, jehož autorem je Janusz A. Brzozowski.

Importujeme

Budeme potřebovat importovat několik modulů, většinu z nich pro parsování výrazu.

import qualified Data.Map as M
import qualified Data.Set as S
import Text.Parsec.Char
import Text.Parsec.String
import Text.Parsec.Combinator
import Text.Parsec.Prim
import Text.Parsec.Expr
import Control.Applicative ((<*), (*>))
import Data.Maybe (fromMaybe)
import Data.List (tails, foldl')

Datové typy

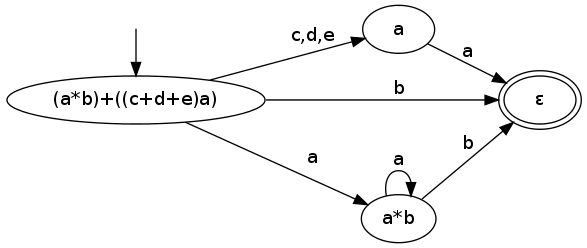
Je potřeba nějak reprezentovat jak samotný regulární výraz, tak i výsledný automat. Regexp je možné reprezentovat jako strom. Listy jsou základní výrazy, uzly potom zřetězení, alternativa a iterace.

Později budeme potřebovat určovat, jestli nějaký regulární výraz popisuje (mimo jiné) prázdné slovo. Pro urychlení tedy u těch konstruktorů, kde to není zřejmé, přidáme tuto informaci.

data Regex a = Epsilon
             | Zero
             | Simple a
             | Plus Bool (Regex a) (Regex a)
             | Conc Bool (Regex a) (Regex a)
             | Iter (Regex a)
             deriving (Eq, Ord, Show)

Pro konečný automat bude potřeba další typ. Automat má nějaké přechody, množinu stavů a počáteční stav. Položka isAccepting je funkce, která pro stav řekne, jestli je akceptující.

type Node = Regex Char  -- ^ Popisek stavu

data FiniteAutomaton = FiniteAutomaton
                     { transitions :: M.Map (Node,Char) Node
                     , states      :: S.Set Node
                     , startNode   :: Node
                     , isAccepting :: Node -> Bool
                     }

V první řadě nadefinujeme tři pomocné funkce pro spojování regexpů, které se postarají o korektní vyplnění pomocné boolovské části a taky zabrání vzniku několika patologických výrazů – např. nemá smysl řetězit něco s prázdným slovem. Jiný příklad je výraz (E*)*, který je ekvivalentní s E* (a navíc vede k zacyklení).

plus :: Regex a -> Regex a -> Regex a
plus Zero x = x
plus x Zero = x
plus x y    = Plus (canBeEpsilon x || canBeEpsilon y) x y

conc :: Regex a -> Regex a -> Regex a
conc Epsilon x = x
conc x Epsilon = x
conc Zero _    = Zero
conc _ Zero    = Zero
conc x y       = Conc (canBeEpsilon x && canBeEpsilon y) x y

iter :: Regex a -> Regex a
iter (Iter x) = Iter x
iter x        = Iter x

Jak jsem psal výše, musíme být schopní pro daný výraz E určit, jestli L(E) obsahuje ϵ. Vzhledem k tomu, kolikrát se tato funkce bude volat při derivování, by bylo dobré, aby dokázala fungovat v konstantním čase.

canBeEpsilon :: Regex a -> Bool
canBeEpsilon Epsilon      = True
canBeEpsilon Zero         = False
canBeEpsilon (Simple _)   = False
canBeEpsilon (Conc e _ _) = e
canBeEpsilon (Plus e _ _) = e
canBeEpsilon (Iter _)     = True

Parsování

A nyní hurá na parsování. Parsec nabízí úžasné možnosti, jak parsovat aritmetické i jiné výrazy. Jediná složitější věc je tady parser pro jednotlivý znak, protože umožňuje využít zpětného lomítka k escapování znaků hvězdičky, plusu a závorek, které by jinak měly speciální význam.

regexP, termP, simpleP :: Parser (Regex Char)
regexP = buildExpressionParser table termP
termP = simpleP <|> char '(' *> regexP <* char ')'
table = [ [ Postfix $ char '*' >> return iter ]
        , [Infix (return conc) AssocLeft]
        , [Infix (char '+' >> return plus) AssocLeft]
        ]
simpleP = do
    c' <- noneOf "()+*"
    c <- if c' == '\\'
            then anyChar
            else return c'
    return (Simple c)

Parser regexP teď můžeme obalit pomocnou funkcí.

fromString :: String -> Regex Char
fromString str = case parse (regexP <* eof) "" str of
    Left _  -> Zero
    Right r -> r

Derivace

Funkce pro derivaci regulárních výrazů je skoro doslovným přepisem definice ze slidů.

derive :: Eq a => Regex a -> a -> Regex a
derive Zero    _      = Zero
derive Epsilon _      = Zero
derive (Simple x) y
    | x == y          = Epsilon
    | otherwise       = Zero
derive (Plus _ p q) x = plus (derive p x) (derive q x)
derive (Conc _ p q) x
    | canBeEpsilon p  = plus (conc (derive p x) q) (derive q x)
    | otherwise       = conc (derive p x) q
derive (Iter p) x     = conc (derive p x) (iter p)

Konstrukce automatu

A můžeme budovat automat! Samotný algoritmus běží v cyklu run, v kterém postupně vytvoříme jak množinu stavů, tak tabulku přechodů.

V každé iteraci vezmeme všechny regulární výrazy z fronty q a každý zderivujeme každým písmenem abecedy. Z těchto všech derivací přidáme nové stavy a přechody mezi ty, co už jsme napočítali. Zároveň nově přidané stavy tvoří novou frontu.

Nemá smysl přidávat žádné hrany, které vedou do stavu odpovídajícího regexpu Zero, tím se jenom zbytečně zvětšuje tabulka přechodů.

toFA :: String -> Regex Char -> FiniteAutomaton
toFA alphabet re = FiniteAutomaton { startNode = re
                                   , transitions = allTransitions
                                   , states = allStates
                                   , isAccepting = canBeEpsilon
                                   }
  where
    (allStates, allTransitions) = run (S.singleton re, M.empty) [re]

    run res []  = res
    run (s,t) q = run (newStates, newTransitions) newQueue
        where
            allD           = [ ((r,a), derive r a) | r <- q, a <- alphabet ]
            derivedStates  = S.fromList $ map snd allD
            newStates      = s `S.union` derivedStates
            newTransitions = M.union t $ M.fromList $ filter ((/= Zero) . snd) allD
            newQueue       = S.toList $ S.difference derivedStates s

Práce s automatem

Když má automat přejít pod nějakým znakem z jednoho stavu do dalšího, podíváme se do tabulky a pokud je přechod nedefinovaný, interpretujeme to jako přechod do stavu Zero.

transition :: FiniteAutomaton -> Node -> Char -> Node
transition fa q a = fromMaybe Zero $ M.lookup (q,a) (transitions fa)

Pro spuštění automatu nad nějakým slovem tedy začneme v počátečním stavu a postupně automat krmíme znaky ze vstupu. Nakonec stačí zkontrolovat, jestli jsme došli do akceptujícího stavu.

runFA :: FiniteAutomaton -> String -> Bool
runFA fa str = isAccepting fa $ foldl' (transition fa) (startNode fa) str

Teď už můžeme zabalit vytváření automatu do jediné funkce.

strToFA :: String -> FiniteAutomaton
strToFA str =  toFA (getAlphabet str) $ fromString str
  where
    getAlphabet = filter (`notElem` "()*+")

Pomocí této funkce můžeme vytvořit jednoduchý operátor, který porovná řetězec s regulárním výrazem E a zjistí, jestli dané slovo patří do L(E).

(=~) :: String -> String -> Bool
str =~ regex = runFA (strToFA regex) str

Nalezení všech odpovídajících podřetězců je maličko složitější. Postupně spustíme automat na všechny sufixy řetězce a zapamatujeme si, kde jsme došli do akceptujícího stavu. Zároveň ale zastavíme, když dorazíme do stavu Zero, protože z něj už není úniku.

allMatches :: RE -> String -> [(Int, Int)]
allMatches re str = concatMap (uncurry $ run 1 (startNode fa)) starts
  where
    fa = strToFA re
    starts = zip [0..] (tails str)

    run _ _    _ []        = []
    run _ Zero _ _         = []
    run end q start (a:as) = let newQ = transition fa q a
                             in if isAccepting fa newQ
                                    then (start, end) : run (end + 1) newQ start as
                                    else                run (end + 1) newQ start as

Další úpravy

V tomhle stavu program při výpočtu tráví naprostou většinu času porovnáváním regulárních výrazů. Bylo by pěkné zbavit se jich a místo nich používat pro označování stavů čísla. To už ale dělat nebudu.

Aktualizace

2012-07-01: upraveno tak, aby (E*)* nevedlo k zacyklení; doplněn odkaz na původní článek